Mudanças entre as edições de "Geometria"
(Criou página com 'Afluentes: Usabilidade, Desenvolvimento Web, Mobile e Jogos') |
|||
| (5 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
| + | |||
Afluentes: [[Usabilidade, Desenvolvimento Web, Mobile e Jogos]] | Afluentes: [[Usabilidade, Desenvolvimento Web, Mobile e Jogos]] | ||
| + | |||
| + | = Introdução = | ||
| + | |||
| + | * '''Geometria''' é a área da matemática que estuda as propriedades e relações das figuras no espaço. | ||
| + | * Fundamental para a '''computação gráfica''', pois permite representar objetos de maneira estruturada. | ||
| + | * Facilita a manipulação e transformação de elementos gráficos em jogos e simulações. | ||
| + | |||
| + | Na computação gráfica, utilizamos conceitos geométricos para modelar cenários, animar personagens e criar efeitos visuais. As principais ferramentas para isso são as coordenadas cartesianas, transformações geométricas e o uso de matrizes para manipulação de objetos. | ||
| + | |||
| + | * Utilizamos escalares, pontos e vetores para representar quantidades, posições e direções. | ||
| + | * Através da combinação de operações sobre esses elementos podemos representar objetos geométricos e realizar o processamento necessário para a síntese de imagens. | ||
| + | |||
| + | = Conceitos Básicos = | ||
| + | |||
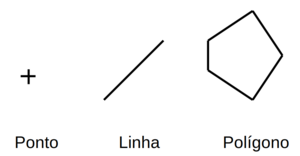
| + | * A base da geometria computacional são os pontos, linhas e polígonos. | ||
| + | * '''Pontos''': elementos espaciais representados por coordenadas. | ||
| + | * '''Linhas''': conectam dois pontos. | ||
| + | * '''Polígonos''': formados por múltiplos segmentos. | ||
| + | |||
| + | [[Arquivo:Ponto linha poligono.png|centro|miniaturadaimagem|Elementos básicos da geometria representados por um ponto no espaço bidimensional, uma reta e um polígono com 5 lados não isométricos.]] | ||
| + | |||
| + | == Coordenadas Cartesianas == | ||
| + | |||
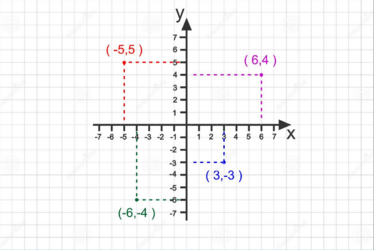
| + | * Um sistema de referência baseado em eixos: | ||
| + | ** X e Y (em 2D) ou | ||
| + | ** X, Y e Z (em 3D) | ||
| + | * Os eixos são usado para posicionar elementos gráficos. | ||
| + | |||
| + | [[Arquivo:Grafico bidimensional coordenadas.png|centro|miniaturadaimagem|374x374px|Gráfico bidimensional contendo o eixo x horizontal, o eixo y, vertical, e alguns pontos aleatórios distribuídos pelo gráfico com sua posição (x, y).]] | ||
| + | A seguir temos um exemplo de programa em python, com o uso da biblioteca pygame, para criar linhas e polígonos. Não estamos desenhando um ponto porque visualmente seria apenas um pixel. Usamos os pontos para criar as linhas e demais elementos.<syntaxhighlight lang="python3"> | ||
| + | import pygame | ||
| + | |||
| + | # Estamos usando a biblioteca pygame. | ||
| + | pygame.init() | ||
| + | |||
| + | screen = pygame.display.set_mode((500, 500)) | ||
| + | clock = pygame.time.Clock() | ||
| + | |||
| + | running = True | ||
| + | while running: | ||
| + | for event in pygame.event.get(): | ||
| + | if event.type == pygame.QUIT: | ||
| + | running = False | ||
| + | |||
| + | screen.fill((255, 255, 255)) | ||
| + | # Desenhamos uma linha na tela, do ponto (30, 50) ao ponto (180, 200) | ||
| + | pygame.draw.line(screen, (255, 0, 0), (30, 50), (180, 200)) | ||
| + | # Desenhamos um poligono ocm base no vetor de pontos passado como parâmetro. | ||
| + | pygame.draw.polygon(screen, (0, 0, 255), [(200, 100), (300, 50), (400, 100), (350, 200), (250, 200)]) | ||
| + | pygame.display.flip() | ||
| + | clock.tick(60) | ||
| + | pygame.quit() | ||
| + | </syntaxhighlight>O código acima gera a representação visual mostrada abaixo. | ||
| + | [[Arquivo:Linhas poligonos python.png|centro|miniaturadaimagem|Imagem resultado da visualização do programa em linguagem de programação python usando biblioteca pygame com uma linha e um polígono de cinco lados.]] | ||
| + | |||
| + | == Espaço Vetorial == | ||
| + | Um espaço vetorial contém um conjunto de escalares e um conjunto de vetores. Usaremos letras minúsculas (a,b,…) para denotar escalares, e letras em negrito (u,v,…) para denotar vetores. | ||
| + | |||
| + | * Um '''escalar''' é um número real ou complexo que representa uma quantidade ou medida. | ||
| + | * Um '''vetor''' é um ente matemático abstrato de um conjunto V fechado para as seguintes operações: | ||
| + | |||
| + | = Transformações Geométricas = | ||
| + | |||
| + | * As transformações geométricas são as alterações na posição, tamanho e orientação de objetos gráficos. As principais são: | ||
| + | ** '''Translação''': Deslocamento de um objeto sem alterar sua forma. | ||
| + | ** '''Rotação''': Giro de um objeto em torno de um ponto específico. | ||
| + | ** '''Escala''': Aumento ou redução do tamanho de um objeto. | ||
| + | |||
| + | {{Tip|Vamos ver mais sobre transformações geométricas no plano (2D) e no espaço (3D) nas próximas aulas.}} | ||
Edição atual tal como às 20h09min de 28 de março de 2025
Afluentes: Usabilidade, Desenvolvimento Web, Mobile e Jogos
Introdução
- Geometria é a área da matemática que estuda as propriedades e relações das figuras no espaço.
- Fundamental para a computação gráfica, pois permite representar objetos de maneira estruturada.
- Facilita a manipulação e transformação de elementos gráficos em jogos e simulações.
Na computação gráfica, utilizamos conceitos geométricos para modelar cenários, animar personagens e criar efeitos visuais. As principais ferramentas para isso são as coordenadas cartesianas, transformações geométricas e o uso de matrizes para manipulação de objetos.
- Utilizamos escalares, pontos e vetores para representar quantidades, posições e direções.
- Através da combinação de operações sobre esses elementos podemos representar objetos geométricos e realizar o processamento necessário para a síntese de imagens.
Conceitos Básicos
- A base da geometria computacional são os pontos, linhas e polígonos.
- Pontos: elementos espaciais representados por coordenadas.
- Linhas: conectam dois pontos.
- Polígonos: formados por múltiplos segmentos.
Coordenadas Cartesianas
- Um sistema de referência baseado em eixos:
- X e Y (em 2D) ou
- X, Y e Z (em 3D)
- Os eixos são usado para posicionar elementos gráficos.
A seguir temos um exemplo de programa em python, com o uso da biblioteca pygame, para criar linhas e polígonos. Não estamos desenhando um ponto porque visualmente seria apenas um pixel. Usamos os pontos para criar as linhas e demais elementos.
import pygame
# Estamos usando a biblioteca pygame.
pygame.init()
screen = pygame.display.set_mode((500, 500))
clock = pygame.time.Clock()
running = True
while running:
for event in pygame.event.get():
if event.type == pygame.QUIT:
running = False
screen.fill((255, 255, 255))
# Desenhamos uma linha na tela, do ponto (30, 50) ao ponto (180, 200)
pygame.draw.line(screen, (255, 0, 0), (30, 50), (180, 200))
# Desenhamos um poligono ocm base no vetor de pontos passado como parâmetro.
pygame.draw.polygon(screen, (0, 0, 255), [(200, 100), (300, 50), (400, 100), (350, 200), (250, 200)])
pygame.display.flip()
clock.tick(60)
pygame.quit()
O código acima gera a representação visual mostrada abaixo.
Espaço Vetorial
Um espaço vetorial contém um conjunto de escalares e um conjunto de vetores. Usaremos letras minúsculas (a,b,…) para denotar escalares, e letras em negrito (u,v,…) para denotar vetores.
- Um escalar é um número real ou complexo que representa uma quantidade ou medida.
- Um vetor é um ente matemático abstrato de um conjunto V fechado para as seguintes operações:
Transformações Geométricas
- As transformações geométricas são as alterações na posição, tamanho e orientação de objetos gráficos. As principais são:
- Translação: Deslocamento de um objeto sem alterar sua forma.
- Rotação: Giro de um objeto em torno de um ponto específico.
- Escala: Aumento ou redução do tamanho de um objeto.
|