Mudanças entre as edições de "Genéticos: Problema da Mochila em Python"
De Aulas
| Linha 9: | Linha 9: | ||
* Resolvido por vários algoritmos | * Resolvido por vários algoritmos | ||
| − | <center>[[Image:Ag_mochila.png]]</center> | + | <center>[[Image:Ag_mochila.png|400px]]</center> |
Podemos representar a '''aptidão''' de uma solução como a soma dos valores dos objetos e com uma penalidade para soluções que passam do limite de volume. | Podemos representar a '''aptidão''' de uma solução como a soma dos valores dos objetos e com uma penalidade para soluções que passam do limite de volume. | ||
Edição das 19h02min de 17 de março de 2022
Afluentes: Inteligência Artificial, Modelos Evolutivos e Tratamento de Incertezas
Definição do Problema
Para mostrar uma implementação de um Algoritmo Genético, iremos trabalhar com o Problema da Mochila.
- Problema de otimização combinatória (NP-Completo)
- Estudado por mais de um século (desde ~1897)
- Resolvido por vários algoritmos
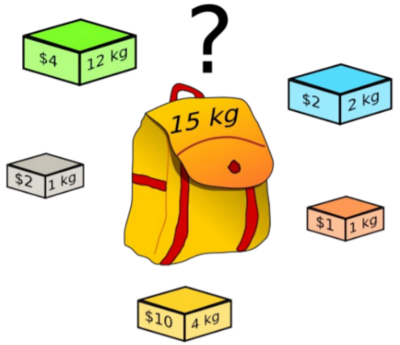
Podemos representar a aptidão de uma solução como a soma dos valores dos objetos e com uma penalidade para soluções que passam do limite de volume.
- Queremos o maior valor possível sem ultrapassar o limite da mochila.
- Vários itens que gostaria de levar em uma mochila
- Cada item tem um peso e um benefício, ou valor
- Há uma capacidade limite de peso
- Deve-se carregar itens com o máximo valor total sem superar o limite de peso
Arquivo de Configuração
1{
2 "capacity": "22",
3 "itens": [
4 { "name": "a", "price": "5", "weight": "7" },
5 { "name": "b", "price": "8", "weight": "8" },
6 { "name": "c", "price": "3", "weight": "4" },
7 { "name": "d", "price": "2", "weight": "10" },
8 { "name": "e", "price": "7", "weight": "4" },
9 { "name": "f", "price": "9", "weight": "6" },
10 { "name": "g", "price": "4", "weight": "4" }
11 ]
12}
Programa em Python
1import json
2from random import *
3
4
5# Lê o arquivo de configuração com a informação dos
6# itens disponíveis, preço e pêso
7def load():
8 config = open('config.json')
9 data = json.load(config)
10 config.close()
11 return data
12
13
14def create_population():
15 global data, population
16 population = []
17 for p in range(population_size):
18 element = []
19 for i in range(len(data["itens"])):
20 # 1 se o elemento está na mochila e 0 se ele está ausente
21 element = element + [randint(0, 1)]
22 element = element + [compute_fitness(element)] # aptidão
23 element = element + [0, 0] # aptidão acumulada e se foi selecionado
24 population = population + [element]
25 # return population
26
27
28def unselect_all():
29 global data, population
30 for i in range(len(population)):
31 population[i][len(data["itens"]) + 2] = 0
32
33def clone_element(element):
34 clone = []
35 for i in range(len(element)):
36 clone += [element[i]]
37 return clone
38
39
40def compute_fitness(element):
41 global data
42 price = 0
43 weight = 0
44 for i in range(len(data["itens"])):
45 if element[i] == 1:
46 price = price + int(data["itens"][i]["price"])
47 weight = weight + int(data["itens"][i]["weight"])
48 fitness = price
49 if weight > int(data["capacity"]):
50 fitness = fitness - 100
51 return fitness
52
53
54def evaluate():
55 global population
56 for i in range(len(population)):
57 compute_fitness(population[i])
58
59
60def selection(best):
61 print("selection", best)
62 unselect_all()
63 global data, population, population_size, selection_size
64 # procura o menor fitness negativo
65 lower = 0
66 fitness_pos = len(data["itens"])
67 for i in range(len(population)):
68 if population[i][fitness_pos] < lower:
69 lower = population[i][fitness_pos]
70
71 # Se houve aptidão negativa, subtrai o menor valor de todos os
72 # elementos para não termos aptidão negativa
73 if lower < 0:
74 for i in range(len(population)):
75 population[i][fitness_pos] = population[i][fitness_pos] - lower
76
77 # ordena a população com base no fitness
78 population = sorted(population, key=lambda x: x[fitness_pos])
79
80 # calcula a aptidão acumulada e aptidão total
81 fitness_total = 0
82 for i in range(len(population)):
83 fitness_total = fitness_total + population[i][fitness_pos]
84 population[i][fitness_pos + 1] = fitness_total
85
86 # seleciona os n melhores. Se for pra escolher quem vai sobreviver
87 # escolhe o tamanho da população
88 aux = selection_size
89 if not best:
90 aux = population_size
91
92 for j in range(aux):
93 last = 0
94 num = randint(0, fitness_total)
95 # encontra a posição da roleta do selecionado
96 found = False
97 i = 0
98 while not found:
99 current = population[i][fitness_pos + 1]
100 if last < num and num <= current:
101 is_selected = population[i][fitness_pos + 2]
102 # se já está selecionado, pega o próximo não selecionado da roleta
103 while is_selected:
104 i = i + 1
105 # se chegou ao final, volta no primeiro
106 if i >= len(population):
107 i = 0
108 is_selected = population[i][fitness_pos + 2]
109 # seleciona
110 population[i][fitness_pos + 2] = 1
111 found = True
112 last = current
113 i += 1
114 if i >= len(population):
115 i = 0
116
117
118def crossover():
119 print("crossover")
120 global data, population, crossover_size, selection_size
121 selected_pos = len(data["itens"]) + 2
122 unselected = []
123 selected = []
124 for i in range(len(population)):
125 if population[i][selected_pos] == 0:
126 unselected = unselected + [population[i]]
127 else:
128 selected = selected + [population[i]]
129 # randomiza para fazer pares aleatórios
130 shuffle(selected)
131 i = 0
132 while i < len(selected):
133 # deseleciona os pais
134 selected[i][selected_pos] = 0
135 selected[i+1][selected_pos] = 0
136 # clona os pais criando os filhos
137 child_a = clone_element(selected[i])
138 child_b = clone_element(selected[i+1])
139 # faz as trocas genéticas
140 for j in range(crossover_size):
141 cross_gen = randint(0, len(data["itens"]) - 1)
142 child_a[cross_gen] = selected[i+1][cross_gen]
143 child_b[cross_gen] = selected[i][cross_gen]
144 compute_fitness(child_a)
145 compute_fitness(child_b)
146 # coloca os filhos criados na lista unselected, que depois
147 # irá compor a população
148 unselected = unselected + [child_a, child_b]
149 i = i + 2
150 population = unselected + selected
151
152
153def mutation():
154 print("mutation")
155 global mutation_elements_size, mutation_size, population, data
156 size = randint(0, mutation_elements_size)
157 for i in range(size):
158 element_pos = randint(1, len(population)) - 1
159 for j in range(mutation_size):
160 mutation_gen = randint(0, len(data["itens"]) - 1)
161 if population[element_pos][mutation_gen] == 1:
162 population[element_pos][mutation_gen] = 0
163 else:
164 population[element_pos][mutation_gen] = 1
165
166
167def survival():
168 print("survival")
169 global population, data
170 selected_pos = len(data["itens"]) + 2
171 aux = population[:]
172 population = []
173 for i in range(len(aux)):
174 if aux[i][selected_pos] == 1:
175 population += [aux[i]]
176
177
178# PROGRAMA PRINCIPAL ------------------------------------------
179data = load()
180population_size = 50
181selection_size = 20
182crossover_size = 2
183mutation_elements_size = 10
184mutation_size = 2
185epochs = 100
186
187create_population()
188for epoch in range(epochs):
189 print("epoch", epoch)
190 selection(True)
191 crossover()
192 mutation()
193 # evaluate()
194 selection(False)
195 survival()
196 # show population
197 for i in range(len(population)):
198 print(population[i])