Computação Gráfica: Transformações em Imagens Matriciais

Afluentes: Computação Gráfica

Transformações Geométricas

As transformações geométricas são operações de processamento de imagem para alterar a posição inicial dos seus píxels. Dentre algumas operações, temos ampliação, diminuição, espelhamento, rotação, distorção, etc.. Veremos alguns deles aqui.

Para nossos testes, iremos utilizar a imagem abaixo:

Alteração de Dimensões

Na alteração de dimensões de uma imagem, alteramos as proporções da saída gravando em arquivo contendo a imagem alterada, seja ela ampliada ou reduzida. Na literatura técnica de processamento de imagens existem dois tipos de alterações de dimensões de uma imagem, embora tecnicamente idênticos:

1. scaling a imagem é ampliada ou reduzida por um fator (que pode ser igual para as dimensões horizontal e vertical / preservando a relação de aspecto original / ou não);
2. sizing (ou resizing) é utilizado nos casos em que, ao invés de especificar o fator de ampliação / redução, o usuário especifica o novo tamanho que a imagem deve possuir.

Se quisermos ampliar a imagem, a nova imagem resultante deve possuir o tamanho necessário para comportá-la. A nova imagem irá conter uma quantidade de pixeis maior do que a original. Então, pelo método mais simples, replicamos os pixeis na nova imagem.

Veja que conforme o tamanho da imagem podemos ter um resultado visual onde podemos observar grandes quadriculados referente aos pixeis de origem. Existem algoritmos para suavizar essa percepção.

Abaixo temos um programa em python que faz um scaling em uma imagem alterando a largura e altura para manter o aspecto original.

 1import sys
 2import pygame
 3
 4# Retorna x e y equivalente da imagem original na destino
 5def get_dest_xy(x_orig, y_orig, proportion):
 6    x = int(proportion * x_orig / 100)  # calcula a regra de tres de x
 7    y = int(proportion * y_orig / 100)  # calcula a regra de tres de y
 8    return x, y
 9
10# Retorna x e y equivalente da imagem destino na original
11def get_orig_xy(x_dest, y_dest, proportion):
12    p = 100 / (proportion / 100)    # pega o percentual invertido
13    x = int(p * x_dest / 100)       # calcula a regra de tres de x
14    y = int(p * y_dest / 100)       # calcula a regra de tres de y
15    return x, y
16
17# Redimensiona a imagem
18def resize(image, surface, proportion):
19    # Para cada coluna da imagem de destino
20    for y in range(surface.get_height()):
21        # Para cada linha da imagem de destino
22        for x in range(surface.get_width()):
23            # pega o x e y relativo da imagem original
24            x2, y2 = get_orig_xy(x, y, proportion)
25            # e pinta na imagem de destino
26            surface.set_at((x, y), image.get_at((x2, y2)))
27
28# PROGRAMA PRINCIPAL
29pygame.init()
30
31file_in = sys.argv[1]
32file_out = sys.argv[2]
33proportion = int(sys.argv[3])
34
35image = pygame.image.load(file_in)
36w = image.get_width()
37h = image.get_height()
38sw, sh = get_dest_xy(w, h, proportion)
39
40# cria a surface com a proporção a ser alterada
41surface = pygame.display.set_mode((sw, sh))
42
43# chama a função pra redimensionar
44resize(image, surface, proportion)
45
46# salva a surface como nova imagem
47pygame.image.save(surface, file_out)
48
49pygame.display.set_caption(file_in)
50
51finish = False
52while not finish:
53    for event in pygame.event.get():
54        if event.type == pygame.QUIT:
55            finish = True
56        elif event.type == pygame.KEYDOWN:
57            if event.key == pygame.K_ESCAPE:
58                finish = True
59    pygame.display.update()
60pygame.quit()
61quit()

Exemplo de execução

python3.9 resize.py imagem.jpg out.jpg 120

O exemplo aumenta a imagem em 20% da original (imagem.jpg), criando uma imagem resultado chamada out.jpg.

Exercício

1. Altere o algoritmo para redimensionar apenas a largura e depois apenas a altura. Observe que a imagem irá ficar espichada.

Espelhamento

A operação de espelhamento consiste em inverter a imagem. No caso do espelhamento horizontal, é como se estivéssemos vendo por um espelho. Quando usamos um espelhamento vertical, a imagem fica de ponta cabeça.

A operação consiste, no caso do horizontal. Para cada píxel de uma linha, ele pega o primeiro e coloca na última posição da imagem de destino. Depois pega o segundo e coloca na penúltima posição. Esse procedimento ocorre até que todos os pixeis da linha tiverem sido colocado na sua respectiva posição da imagem de destino. Depois segue para a próxima linha até que toda a imagem tenha sido rasterizada.

O programa em python abaixo faz o espelhamento horizontal da imagem.

 1import sys
 2import pygame
 3
 4# Função de espelhamento. O resultado é colocado em surface
 5def flip(image, surface):
 6    w = image.get_width()
 7    h = image.get_height()
 8    for y in range(h):
 9        for x in range(w):
10            # coloca o último pixel na primeira posição,
11            # o penúltimo na segunda, e assim por diante.
12            surface.set_at((w - 1 - x, y), image.get_at((x, y)))
13
14
15# PROGRAMA PRINCIPAL
16pygame.init()
17
18file_in = sys.argv[1]
19file_out = sys.argv[2]
20
21image = pygame.image.load(file_in)
22w = image.get_width()
23h = image.get_height()
24
25# cria a surface com a proporção a ser alterada
26surface = pygame.display.set_mode((w, h))
27
28# chama a função fazer o espelhamento
29flip(image, surface)
30
31# salva a imagem
32pygame.image.save(surface, file_out)
33
34pygame.display.set_caption(file_in)
35
36finish = False
37while not finish:
38    for event in pygame.event.get():
39        if event.type == pygame.QUIT:
40            finish = True
41        elif event.type == pygame.KEYDOWN:
42            if event.key == pygame.K_ESCAPE:
43                finish = True
44    pygame.display.update()
45pygame.quit()
46quit()

Execução

python3.9 flip.py image.jpg flip.jpg

Exercícios

1. Altere o programa para fazer o espelhamento vertical da imagem.

Rotação

Uma imagem pode ser rotacionada de um ângulo arbitrário, tanto no sentido horário quanto no anti-horário. Rotações com ângulos múltiplos de 90º são mais simples de implementar, pois consistem na cópia de pixels que estão organizados em linhas, reordenando-os em colunas na direção em que se deseja rotacionar a imagem. A figura 25 ilustra o processo de rotação de 90º no sentido horário. A área tracejada destaca as primeiras linhas da imagem original, que são reposicionadas em formas de colunas, da direita para a esquerda, na imagem rotacionada.

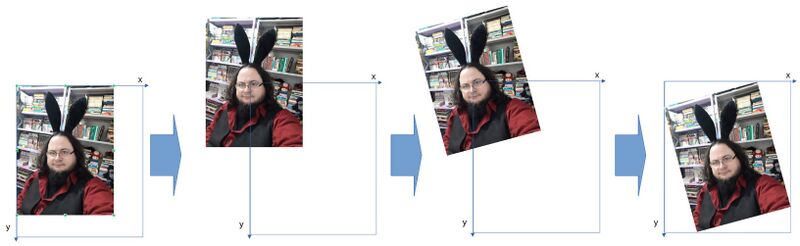
Rotações diferentes requerem operações mais complexas, como no caso do exemplo a seguir em que a imagem foi rotacionada em 15º.

Observe que quando rotacionamos, tanto a largura quanto a altura são aumentadas para comportar a imagem em sua totalidade. Logo, a imagem resultante será maior que a original.

Para calcular o tamanho da nova imagem, precisamos rotacionar os vértices da imagem original pelo ângulo requerido. Depois pegamos o x mínimo de todos os vértices, o x máximo, assim como o y mínimo e o y máximo. Então teremos o tamanho da imagem como:

$w=x\_max-x\_min$

$h=y\_max-y\_min$

Ok, com isso temos a largura e altura da nova imagem. Contudo, ainda não vimos a fórmula da rotação.

A operação de rotação ocorre com a multiplicação da matriz de Rotação com todos os píxeis da imagem. Porém, é importante observar que a matriz de rotação, no caso de uma imagem matricial, é apenas nos eixos x e y. No espaço tridimensional, temos a rotação em todos os eixos (x, y e z). Dessa forma, as matrizes de rotação são apresentadas a seguir:

${\begin{pmatrix}\cos(\theta )&\sin(\theta )\\-\sin(\theta )&\cos(\theta )\\\end{pmatrix}}$

tal que:

θ é o ângulo, em radianos, que se quer rotacionar o objeto,
sin é a operação do seno sobre o ângulo e
cos é a operação do cosseno sobre o ângulo.

Logo, a fórmula matemática da operação de translação fica da seguinte forma:

${\begin{pmatrix}x&y\end{pmatrix}}\cdot {\begin{pmatrix}\cos(\theta )&\sin(\theta )\\-\sin(\theta )&\cos(\theta )\\\end{pmatrix}}$

tal que:

$x'=(x\cdot \cos(\theta ))+(y\cdot -\sin(\theta ))$

$y'=(x\cdot \sin(\theta ))+(y\cdot \cos(\theta ))$

Um problema é que se simplesmente rotacionarmos a imagem, ela irá se basear no seu ponto de origem (0, 0). Então vários pontos acabam saindo da área onde a imagem deve ser representada.

Dessa forma, precisamos mover nosso ponto de origem para o meio da imagem. Ou melhor, movemos a imagem para que seu ponto de origem coincida com o ponto (0, 0). Essa é uma operação de translação.

A operação da translação ocorre com a soma da matriz de translação com todos os pontos do objeto. A matriz de translação é a seguinte:

${\begin{pmatrix}Tx&Ty\end{pmatrix}}$

tal que:

Tx é a translação na horizontal e
Ty é a translação na vertical

Logo, a fórmula matemática da operação de translação fica da seguinte forma:

${\begin{pmatrix}x&y\end{pmatrix}}+{\begin{pmatrix}Tx&Ty\end{pmatrix}}$

tal que:

$x=x+Tx$

$y=y+Ty$

Com a fórmula da translação, então devemos fazer o seguinte:

1. Para cada ponto da imagem
   1. Pego o meio da imagem original
   2. translado para o negativo do meio da imagem original
   3. rotaciono o ponto
   4. translado considerando o meio da imagem de destino