Mudanças entre as edições de "Perceptron"
| Linha 1: | Linha 1: | ||
| + | |||
Afluentes: | Afluentes: | ||
* [[Inteligência Artificial]] | * [[Inteligência Artificial]] | ||
| Linha 177: | Linha 178: | ||
Tendo feito ou não os ajustes dos pesos, segue-se para o próximo exemplo. Quando terminar a execução de todos os exemplos é completada uma época. | Tendo feito ou não os ajustes dos pesos, segue-se para o próximo exemplo. Quando terminar a execução de todos os exemplos é completada uma época. | ||
| − | O algoritmo deve continuar até que não não seja mais necessário ajustar os pesos. Nesse caso, diz-se que o neurônio esta treinado. Também deve-se definir um limite de épocas, caso o algoritmo não convergir, ou seja, não conseguir treinar. Isso previne que o algoritmo fique indefinidamente treinando sem nunca conseguir convergir | + | O algoritmo deve continuar até que não não seja mais necessário ajustar os pesos. Nesse caso, diz-se que o neurônio esta treinado. Também deve-se definir um limite de épocas, caso o algoritmo não convergir, ou seja, não conseguir treinar. Isso previne que o algoritmo fique indefinidamente treinando sem nunca conseguir convergir. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Edição atual tal como às 10h33min de 29 de junho de 2024
Afluentes:
O Neurônio Artificial
O neurônio artificial é um modelo simplificado e simulado do neurônio real e suas características básicas são a adaptação e a representação de conhecimentos baseada em conexões.
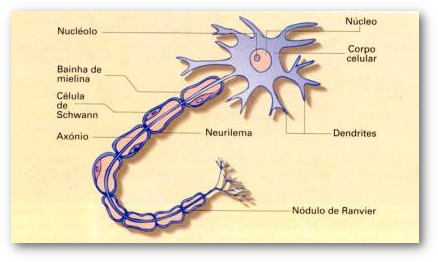
O Modelo de McCulloch & Pitts (1943)
- Viu-se o cérebro como um sistema computacional.
- Este modelo é uma simplificação do que se sabia então a respeito do neurônio biológico.
Suposições básicas
- A atividade de um neurônio é um processo tudo ou nada.
- Um certo número fixo (>1) de entradas devem ser excitadas dentro de um período de adição latente para excitar um neurônio.
- Único atraso significativo é o atraso sináptico.
- A atividade de qualquer sinapse inibitória previne absolutamente a excitação do neurônio.
- A estrutura das interconexões não muda com o tempo.
Descrição matemática
- Tem-se o neurônio com n terminais de entrada x1, x2,... xn (dendritos) e apenas um terminal de saída y (axônio).
- O comportamento das sinapses é emulado através de pesos w1, w2,..., wn acoplados as entradas dos neurônios, cujo valor pode ser excitatório ou inibitório.
- O efeito de uma sinapse i no neurônio pós-sináptico é dado por xiwi.
Elementos Básicos de um Neurônio Artificial
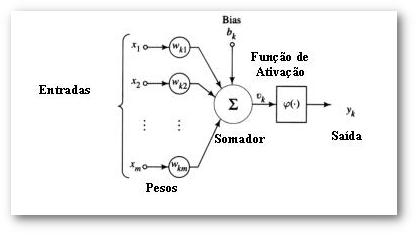
Entradas
- As entradas podem ser as saídas de outros neurônios, entradas extrenas, um bias ou qualquer combinação destes elementos.
- Bias (Tendência) é um erro sistemático diferentemente de erro aleatório. Um ou mais componentes do erro sistemático podem contribuir para a tendência. Uma grande diferença sistemática em relação ao valor de referência aceito reflete-se em um grande valor de tendência.
A Combinação das Entradas - O "Net"
O somatório de todas estas entradas, multiplicadas por suas respectivas forças de conexão sináptica (os pesos), dá origem ao chamado "net" de um neurônio.
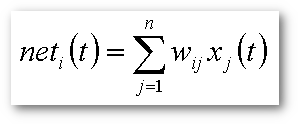
wij é um número real que representa a conexão sináptica da entrada j-ésimo neurônio. A conexão sináptica é conhecida como excitatória se wij>0 ou inibitória caso wij<0.
Após a determinação do net, o valor da ativação do neurônio é atualizado através da função de ativação fa e finalmente, o valor de saída do neurônio é produzido através da função de saída fs.
Função de Ativação (fa)
x(t+1) = fa (x(t), net(t))
- Os estados futuros de um neurônio são afetados pelo estado atual do neurônio e pelo valor do net de entrada. Este tipo de neurônio, que possui "memória" é conhecido como neurônio dinâmico.
- Por outro lado, se considerarmos a função como constante, teremos neurônios que não possuem "memória", ou seja, o estado atual é igual aos estados anteriores e portanto o neurônio é considerado como "neurônio estático".
2.4. Função de Saída (fs):
- Essencialmente, qualquer função contínua e monotômica crescente, tal que x E R e y(x) E [-1,1], pode ser utilizada como função de saída na modelagem neural.
- Existem uma série de funções mais comumente utilizadas como funções de saída em neurônios. Estas funções são:
- A Função Linear y(x) = ax
- A Função Sigmoidal ou Logística y(x) = 1 / (1 + e-kx)
- A Função Tangente Hiperbólica y(x) = tanh(kx) = (1 - e-kx) / (1 + e-kx)
Algoritmo
Esta implementação simples de um neurônio artificial para portas lógicas é composto básicamente de uma entrada "bias" com valor "-1", duas entradas e a saída. O "bias" é um elemento que serve para aumentar o grau de liberdade dos ajustes dos pesos.
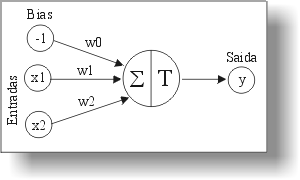
Os valores de w, x e y precisam estar em um domínio específico.
domínio de w = [-1, 1] domínio de x = [ 0, 1] domínio de y = [ 0, 1]
A execução do neurônio se dá pelo somatório de todas as suas entradas multiplicadas por seus pesos sinápticos passados por uma função de transferência "T".

Após a saída do net, o valor é jogado na função de transferência T, retornando então o resultado final y.
se net > 0 então y = 1 senão y = 0
A seguir é apresentada a fórmula para ajustes dos pesos do neurônio artificia e deve ser aplicada à todos os pesos de todas as entradas caso o resultado y que resultou da execução do neurônio seja diferente do resultado esperado. Esta fórmula é específica para o treinamento do neurônio artificial.

Treinamento
início atribuir pesos aleatórios laço para cada exemplo fazer executar exemplo se saida incorreta então fazer modificar pesos (w) fim se fim para repetir até (todas saídas corretas) ou (terminar N épocas) fim
Exemplo
Para descobrir o net, é necessário fazer o cálculo do neurônio para todas suas entradas. Por exemplo, considere que esteja sendo feito o treinamento do neuronio para aprender a operação lógica OU. Para cada conjunto de entradas e saida é necessário testar:
y = Transferência(Net)
Observe que para a operação OU tem-se os seguintes exemplos (conjuntos de entradas e saída):
1 - entradas 0 e 0 - saída 0 2 - entradas 0 e 1 - saída 1 3 - entradas 1 e 0 - saída 1 4 - entradas 1 e 1 - saída 1
Para cada um desses 4 conjuntos (exemplos), deve-se executar o neurônio.
Para exemplificar, peguemos peguemos o exemplo 2, onde as entradas são 0 e 1 e a saída é 1):
x0 = bias = -1 w0 = 0,7 x1 = 0 w1 = -0,3 x2 = 1 w2 = 0,4
Se executarmos o Net, então teremos o seguinte:
Net = x0 X w0 + x1 X w1 + x2 X w2. Net = (-1) X 0,7 + 0 X (-0,3) + 1 X 0,4 Net = -0,7 + 0 + 0,4 Net = -0,3
Aplicando a função de Transferência, teremos:
Se Net > 0, então y = 1, senão y = 0
Sendo assim teremos o resultado da execução do neurônio em y:
y = 0; (deveria ter dado 1)
Neste caso, o y retornado está errado. Dessa forma é necessário usar o algoritmo de ajuste dos pesos para todos os pesos de todas as entradas do neurônio.
fórmula de ajuste de pesos: wi = wi + N(t - y)xi (considerando que N = 0,1)
w0 = 0,7 + 0,1(1 - 0) * (-1) = 0,6 w1 = -0,3 + 0,1(1 - 0) * 0 = -0,3 w2 = 0,4 + 0,1(1 - 0) * 1 = 0,5
Logo, os novos pesos são:
w0 = 0,6 w1 = -0,3 w2 = 0,5
Tendo feito ou não os ajustes dos pesos, segue-se para o próximo exemplo. Quando terminar a execução de todos os exemplos é completada uma época.
O algoritmo deve continuar até que não não seja mais necessário ajustar os pesos. Nesse caso, diz-se que o neurônio esta treinado. Também deve-se definir um limite de épocas, caso o algoritmo não convergir, ou seja, não conseguir treinar. Isso previne que o algoritmo fique indefinidamente treinando sem nunca conseguir convergir.