Mudanças entre as edições de "Genéticos: Problema da Mochila em Python"

De Aulas
 
(19 revisões intermediárias pelo mesmo usuário não estão sendo mostradas)
Linha 1: Linha 1:
 +
 
Afluentes: [[Inteligência Artificial]], [[Modelos Evolutivos e Tratamento de Incertezas]]
 
Afluentes: [[Inteligência Artificial]], [[Modelos Evolutivos e Tratamento de Incertezas]]
  
Linha 4: Linha 5:
  
 
Para mostrar uma implementação de um Algoritmo Genético, iremos trabalhar com o '''Problema da Mochila'''.
 
Para mostrar uma implementação de um Algoritmo Genético, iremos trabalhar com o '''Problema da Mochila'''.
 +
 +
Sobre o problema da mochila:
  
 
* Problema de otimização combinatória (NP-Completo)
 
* Problema de otimização combinatória (NP-Completo)
Linha 11: Linha 14:
 
<center>[[Image:Ag_mochila.png|400px]]</center>
 
<center>[[Image:Ag_mochila.png|400px]]</center>
  
−
Podemos representar a '''aptidão''' de uma solução como a soma dos valores dos objetos e com uma penalidade para soluções que passam do limite de volume.
+
Podemos representar a aptidão de uma solução como a soma dos valores dos objetos e com uma penalidade para soluções que passam do limite de volume.
  
 
* Queremos o maior valor possível sem ultrapassar o limite da mochila.
 
* Queremos o maior valor possível sem ultrapassar o limite da mochila.
 
* Vários itens que gostaria de levar em uma mochila
 
* Vários itens que gostaria de levar em uma mochila
 
* Cada item tem um peso e um benefício, ou valor
 
* Cada item tem um peso e um benefício, ou valor
−
* Há uma capacidade limite de peso
+
* Existe uma capacidade limite de peso
 
* Deve-se carregar itens com o máximo valor total sem superar o limite de peso
 
* Deve-se carregar itens com o máximo valor total sem superar o limite de peso
−
 
−
= Arquivo de Configuração =
 
−
 
−
<syntaxhighlight lang=json line>
 
−
{
 
−
  "capacity": "22",
 
−
  "itens": [
 
−
    { "name": "a", "price": "5", "weight": "7" },
 
−
    { "name": "b", "price": "8", "weight": "8" },
 
−
    { "name": "c", "price": "3", "weight": "4" },
 
−
    { "name": "d", "price": "2", "weight": "10" },
 
−
    { "name": "e", "price": "7", "weight": "4" },
 
−
    { "name": "f", "price": "9", "weight": "6" },
 
−
    { "name": "g", "price": "4", "weight": "4" }
 
−
  ]
 
−
}
 
−
</syntaxhighlight>
 
  
 
= Programa em Python =
 
= Programa em Python =
  
−
<syntaxhighlight lang=Python line>
+
Coloquei o programa no github, fica mais fácil, fazer atualizações, de baixar e bom para visualizar. Vejam que o programa deu quase 300 linhas, mas é porque está todo comentado. Se tirar os comentários ele fica bem menor. É um algoritmo muito fácil e simples, talvez um dos mais fáceis de se implementar da Inteligência Artificial.
−
import json
 
−
from random import *
 
  
 +
'''Link do github''': https://github.com/saulopz/ia_genetico_mochila
  
−
# Lê o arquivo de configuração com a informação dos
+
Para baixar em seu computador, basta executar o comando:
−
# itens disponíveis, preço e pêso
 
−
def load():
 
−
    config = open('config.json')
 
−
    data = json.load(config)
 
−
    config.close()
 
−
    return data
 
  
 +
git clone https://github.com/saulopz/ia_genetico_mochila
  
−
def create_population():
+
{{tip|Eu estava fazendo procedural e estava tendo que fazer uns remendos, como encher de variáveis globais e outras coisas mais, e acho que isso estava permitindo um bug difícil de encontrar. Então decidi ir pra orientação a objetos que pra mim é mais fácil de entender e organizar. A ideia do algoritmo é a mesma que expliquei, mesmas funções, mesmaa funcionalidade, só está organizado como objetos. E, no final, era um bug bobo mesmo por causa de variáveis globais.}}
−
    global data, population
 
−
    population = []
 
−
    for p in range(population_size):
 
−
        element = []
 
−
        for i in range(len(data["itens"])):
 
−
            # 1 se o elemento está na mochila e 0 se ele está ausente
 
−
            element = element + [randint(0, 1)]
 
−
        element = element + [compute_fitness(element)]  # aptidão
 
−
        element = element + [0, 0]  # aptidão acumulada e se foi selecionado
 
−
        population = population + [element]
 
−
    # return population
 
  
 +
== Solução ==
  
−
def unselect_all():
+
A solução encontrada para o algoritmo com os parâmetros e configuração acima fica:
−
    global data, population
 
−
    for i in range(len(population)):
 
−
        population[i][len(data["itens"]) + 2] = 0
 
  
−
def clone_element(element):
+
<pre>
−
    clone = []
+
SOLUÇÃO ------------------------------
−
    for i in range(len(element)):
+
Capacidade da mochila: 22
−
        clone += [element[i]]
+
- tv valor: 8 gold - peso: 8
−
    return clone
+
- colar valor: 7 gold - peso: 4
 +
- videogame valor: 9 gold - peso: 6
 +
- smarthone valor: 4 gold - peso: 4
 +
Valor total: 28 gold
 +
Peso total : 22
 +
--------------------------------------
 +
</pre>
  
 +
== Alterações para novo teste ==
  
−
def compute_fitness(element):
+
No arquivo config.json adicionei um item (impressora) no arquivo de configuração e aumentei a capacidade para 25. Também alterei as variáveis do algoritmo aumentando a população, gerações, etc.
−
    global data
 
−
    price = 0
 
−
    weight = 0
 
−
    for i in range(len(data["itens"])):
 
−
        if element[i] == 1:
 
−
            price = price + int(data["itens"][i]["price"])
 
−
            weight = weight + int(data["itens"][i]["weight"])
 
−
    fitness = price
 
−
    if weight > int(data["capacity"]):
 
−
        fitness = fitness - 100
 
−
    return fitness
 
  
 +
<syntaxhighlight lang="json">
 +
{
 +
  "population_size": "100",
 +
  "selection_size": "40",
 +
  "crossover_gene_size": "2",
 +
  "mutation_individual_size": "20",
 +
  "mutation_gene_size": "2",
 +
  "generations": "500",
 +
  "penality": "100",
  
−
def evaluate():
+
  "capacity": "25",
−
    global population
+
  "items": [
−
     for i in range(len(population)):
+
     { "name": "notebook", "value": "5", "weight": "7" },
−
        compute_fitness(population[i])
+
     { "name": "tv", "value": "8", "weight": "8" },
−
 
+
     { "name": "tablet", "value": "3", "weight": "4" },
−
 
+
     { "name": "anel", "value": "2", "weight": "10" },
−
def selection(best):
+
     { "name": "colar", "value": "7", "weight": "4" },
−
     print("selection", best)
+
     { "name": "videogame", "value": "9", "weight": "6" },
−
     unselect_all()
+
     { "name": "smarthone", "value": "4", "weight": "1" },
−
     global data, population, population_size, selection_size
+
     { "name": "impressora", "value": "2", "weight": "5" }
−
     # procura o menor fitness negativo
+
  ]
−
     lower = 0
+
}
−
     fitness_pos = len(data["itens"])
+
</syntaxhighlight>
−
    for i in range(len(population)):
 
−
        if population[i][fitness_pos] < lower:
 
−
            lower = population[i][fitness_pos]
 
−
 
 
−
     # Se houve aptidão negativa, subtrai o menor valor de todos os
 
−
    # elementos para não termos aptidão negativa
 
−
    if lower < 0:
 
−
        for i in range(len(population)):
 
−
            population[i][fitness_pos] = population[i][fitness_pos] - lower
 
−
 
 
−
    # ordena a população com base no fitness
 
−
    population = sorted(population, key=lambda x: x[fitness_pos])
 
  
−
    # calcula a aptidão acumulada e aptidão total
+
E obtive a seguinte solução:
−
    fitness_total = 0
 
−
    for i in range(len(population)):
 
−
        fitness_total = fitness_total + population[i][fitness_pos]
 
−
        population[i][fitness_pos + 1] = fitness_total
 
  
−
    # seleciona os n melhores. Se for pra escolher quem vai sobreviver
+
<pre>
−
    # escolhe o tamanho da população
+
SOLUÇÃO ------------------------------
−
    aux = selection_size
+
Capacidade da mochila: 25
−
    if not best:
+
- notebook valor: 5 gold - peso: 7
−
        aux = population_size
+
- tv valor: 8 gold - peso: 8
 +
- colar valor: 7 gold - peso: 4
 +
- videogame valor: 9 gold - peso: 6
 +
Valor total: 29 gold
 +
Peso total : 25
 +
--------------------------------------
 +
</pre>
  
−
    for j in range(aux):
+
A partir daí, dá para gente ir brincando com as configurações do algoritmo, informações do problema e outras variáveis para ver como os resultados vão se alterando.
−
        last = 0
 
−
        num = randint(0, fitness_total)
 
−
        # encontra a posição da roleta do selecionado
 
−
        found = False
 
−
        i = 0
 
−
        while not found:
 
−
            current = population[i][fitness_pos + 1]
 
−
            if last < num and num <= current:
 
−
                is_selected = population[i][fitness_pos + 2]
 
−
                # se já está selecionado, pega o próximo não selecionado da roleta
 
−
                while is_selected:
 
−
                    i = i + 1
 
−
                    # se chegou ao final, volta no primeiro
 
−
                    if i >= len(population):
 
−
                        i = 0
 
−
                    is_selected = population[i][fitness_pos + 2]
 
−
                # seleciona
 
−
                population[i][fitness_pos + 2] = 1
 
−
                found = True
 
−
            last = current
 
−
            i += 1
 
−
            if i >= len(population):
 
−
                i = 0
 
−
 
 
−
 
 
−
def crossover():
 
−
    print("crossover")
 
−
    global data, population, crossover_size, selection_size
 
−
    selected_pos = len(data["itens"]) + 2
 
−
    unselected = []
 
−
    selected = []
 
−
    for i in range(len(population)):
 
−
        if population[i][selected_pos] == 0:
 
−
            unselected = unselected + [population[i]]
 
−
        else:
 
−
            selected = selected + [population[i]]
 
−
    # randomiza para fazer pares aleatórios
 
−
    shuffle(selected)
 
−
    i = 0
 
−
    while i < len(selected):
 
−
        # deseleciona os pais
 
−
        selected[i][selected_pos] = 0
 
−
        selected[i+1][selected_pos] = 0
 
−
        # clona os pais criando os filhos
 
−
        child_a = clone_element(selected[i])
 
−
        child_b = clone_element(selected[i+1])
 
−
        # faz as trocas genéticas
 
−
        for j in range(crossover_size):
 
−
            cross_gen = randint(0, len(data["itens"]) - 1)
 
−
            child_a[cross_gen] = selected[i+1][cross_gen]
 
−
            child_b[cross_gen] = selected[i][cross_gen]
 
−
        compute_fitness(child_a)
 
−
        compute_fitness(child_b)
 
−
        # coloca os filhos criados na lista unselected, que depois
 
−
        # irá compor a população
 
−
        unselected = unselected + [child_a, child_b]
 
−
        i = i + 2
 
−
    population = unselected + selected
 
−
 
 
−
 
 
−
def mutation():
 
−
    print("mutation")
 
−
    global mutation_elements_size, mutation_size, population, data
 
−
    size = randint(0, mutation_elements_size)
 
−
    for i in range(size):
 
−
        element_pos = randint(1, len(population)) - 1
 
−
        for j in range(mutation_size):
 
−
            mutation_gen = randint(0, len(data["itens"]) - 1)
 
−
            if population[element_pos][mutation_gen] == 1:
 
−
                population[element_pos][mutation_gen] = 0
 
−
            else:
 
−
                population[element_pos][mutation_gen] = 1
 
−
 
 
−
 
 
−
def survival():
 
−
    print("survival")
 
−
    global population, data
 
−
    selected_pos = len(data["itens"]) + 2
 
−
    aux = population[:]
 
−
    population = []
 
−
    for i in range(len(aux)):
 
−
        if aux[i][selected_pos] == 1:
 
−
            population += [aux[i]]
 
−
 
 
−
 
 
−
# PROGRAMA PRINCIPAL ------------------------------------------
 
−
data = load()
 
−
population_size = 50
 
−
selection_size = 20
 
−
crossover_size = 2
 
−
mutation_elements_size = 10
 
−
mutation_size = 2
 
−
epochs = 100
 
−
 
 
−
create_population()
 
−
for epoch in range(epochs):
 
−
    print("epoch", epoch)
 
−
    selection(True)
 
−
    crossover()
 
−
    mutation()
 
−
    # evaluate()
 
−
    selection(False)
 
−
    survival()
 
−
    # show population
 
−
    for i in range(len(population)):
 
−
        print(population[i])
 
−
</syntaxhighlight>
 

Edição atual tal como às 19h45min de 7 de junho de 2024

Afluentes: Inteligência Artificial, Modelos Evolutivos e Tratamento de Incertezas

Definição do Problema

Para mostrar uma implementação de um Algoritmo Genético, iremos trabalhar com o Problema da Mochila.

Sobre o problema da mochila:

  • Problema de otimização combinatória (NP-Completo)
  • Estudado por mais de um século (desde ~1897)
  • Resolvido por vários algoritmos
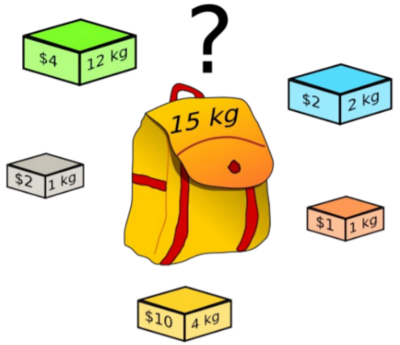
Ag mochila.png

Podemos representar a aptidão de uma solução como a soma dos valores dos objetos e com uma penalidade para soluções que passam do limite de volume.

  • Queremos o maior valor possível sem ultrapassar o limite da mochila.
  • Vários itens que gostaria de levar em uma mochila
  • Cada item tem um peso e um benefício, ou valor
  • Existe uma capacidade limite de peso
  • Deve-se carregar itens com o máximo valor total sem superar o limite de peso

Programa em Python

Coloquei o programa no github, fica mais fácil, fazer atualizações, de baixar e bom para visualizar. Vejam que o programa deu quase 300 linhas, mas é porque está todo comentado. Se tirar os comentários ele fica bem menor. É um algoritmo muito fácil e simples, talvez um dos mais fáceis de se implementar da Inteligência Artificial.

Link do github: https://github.com/saulopz/ia_genetico_mochila

Para baixar em seu computador, basta executar o comando: 

git clone https://github.com/saulopz/ia_genetico_mochila


Tplnote Bulbgraph.png

Eu estava fazendo procedural e estava tendo que fazer uns remendos, como encher de variáveis globais e outras coisas mais, e acho que isso estava permitindo um bug difícil de encontrar. Então decidi ir pra orientação a objetos que pra mim é mais fácil de entender e organizar. A ideia do algoritmo é a mesma que expliquei, mesmas funções, mesmaa funcionalidade, só está organizado como objetos. E, no final, era um bug bobo mesmo por causa de variáveis globais.

Solução

A solução encontrada para o algoritmo com os parâmetros e configuração acima fica: 

SOLUÇÃO ------------------------------
Capacidade da mochila: 22
- tv valor: 8 gold - peso: 8
- colar valor: 7 gold - peso: 4
- videogame valor: 9 gold - peso: 6
- smarthone valor: 4 gold - peso: 4
Valor total: 28 gold
Peso total : 22
--------------------------------------

Alterações para novo teste

No arquivo config.json adicionei um item (impressora) no arquivo de configuração e aumentei a capacidade para 25. Também alterei as variáveis do algoritmo aumentando a população, gerações, etc. 

{
  "population_size": "100",
  "selection_size": "40",
  "crossover_gene_size": "2",
  "mutation_individual_size": "20",
  "mutation_gene_size": "2",
  "generations": "500",
  "penality": "100",

  "capacity": "25",
  "items": [
    { "name": "notebook", "value": "5", "weight": "7" },
    { "name": "tv", "value": "8", "weight": "8" },
    { "name": "tablet", "value": "3", "weight": "4" },
    { "name": "anel", "value": "2", "weight": "10" },
    { "name": "colar", "value": "7", "weight": "4" },
    { "name": "videogame", "value": "9", "weight": "6" },
    { "name": "smarthone", "value": "4", "weight": "1" },
    { "name": "impressora", "value": "2", "weight": "5" }
  ]
}

E obtive a seguinte solução: 

SOLUÇÃO ------------------------------
Capacidade da mochila: 25
- notebook valor: 5 gold - peso: 7
- tv valor: 8 gold - peso: 8
- colar valor: 7 gold - peso: 4
- videogame valor: 9 gold - peso: 6
Valor total: 29 gold
Peso total : 25
--------------------------------------

A partir daí, dá para gente ir brincando com as configurações do algoritmo, informações do problema e outras variáveis para ver como os resultados vão se alterando.

Disponível em “https://saulo.arisa.com.br/wiki/index.php?title=Genéticos:_Problema_da_Mochila_em_Python&oldid=9447”