Mudanças entre as edições de "Transformações em Imagens Vetoriais no Plano"
(→Escala) |
(→Escala) |
||
| (6 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 42: | Linha 42: | ||
== Translação == | == Translação == | ||
| − | + | A translação no plano é a operação que move determinado objeto de um local à outro no no espaço bidimensional. A operação da translação ocorre com a soma da matriz de translação com todos os pontos do objeto. A matriz de translação é a seguinte: | |
| − | + | <math> | |
| − | + | \begin{pmatrix} | |
| − | < | + | Tx & Ty |
| − | + | \end{pmatrix} | |
| − | </ | + | </math> |
tal que: | tal que: | ||
| − | + | Tx é a translação na horizontal e | |
| − | + | Ty é a translação na vertical. | |
| − | |||
| − | |||
Logo, a fórmula matemática da operação de translação fica da seguinte forma: | Logo, a fórmula matemática da operação de translação fica da seguinte forma: | ||
| − | < | + | <math> |
| − | + | \begin{pmatrix} x & y \end{pmatrix} \cdot \begin{pmatrix} Tx & Ty \end{pmatrix} | |
| − | </ | + | </math> |
tal que: | tal que: | ||
| − | < | + | <math> |
x = x + Tx | x = x + Tx | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
y = y + Ty | y = y + Ty | ||
| − | </ | + | </math> |
=== Algoritmo === | === Algoritmo === | ||
| Linha 117: | Linha 118: | ||
A operação da escala ocorre com a multiplicação da matriz de Escala com todos os pontos do objeto. A matriz de escala é a seguinte: | A operação da escala ocorre com a multiplicação da matriz de Escala com todos os pontos do objeto. A matriz de escala é a seguinte: | ||
| − | < | + | <math> |
| − | + | \begin{pmatrix} | |
| − | + | Sx & 0 \\ | |
| − | </ | + | 0 & Sy |
| + | \end{pmatrix} | ||
| + | </math> | ||
tal que: | tal que: | ||
| − | + | ''Sx'' : é a modificação da escala na horizontal e | |
| − | + | ''Sy'' : é a modificação da escala na vertical. | |
| − | |||
| − | |||
Logo, a fórmula matemática da operação de translação fica da seguinte forma: | Logo, a fórmula matemática da operação de translação fica da seguinte forma: | ||
| − | < | + | <math> |
| − | + | \begin{pmatrix} | |
| − | + | x & y | |
| − | </ | + | \end{pmatrix} |
| + | \cdot | ||
| + | \begin{pmatrix} | ||
| + | Sx & 0 \\ | ||
| + | 0 & Sy | ||
| + | \end{pmatrix} | ||
| + | </math> | ||
tal que: | tal que: | ||
| − | < | + | <math> |
| − | x = (x | + | x = (x \cdot Sx) + (y \cdot 0) = x \cdot Sx |
| − | y = (x | + | </math> |
| − | </ | + | |
| + | <math> | ||
| + | y = (x \cdot 0) + (y \cdot Sy) = y \cdot Sy | ||
| + | </math> | ||
=== Algoritmo === | === Algoritmo === | ||
| Linha 234: | Linha 244: | ||
== Rotação == | == Rotação == | ||
| − | + | A rotação, no plano, é a operação que rotaciona determinado objeto no espaço bidimensional. A operação de rotação ocorre com a multiplicação da matriz de Rotação com todos os pontos do objeto. A matriz de rotação é a seguinte: | |
| − | + | <center>[[Image:Circle_sincos.gif]]</center> | |
| − | < | + | <math> |
| − | + | \begin{pmatrix} | |
| − | + | \cos(\theta) & \sin(\theta) \\ | |
| − | </ | + | -\sin(\theta) & \cos(\theta) \\ |
| + | \end{pmatrix} | ||
| + | </math> | ||
tal que: | tal que: | ||
| − | + | ''θ'' é o ângulo, '''em radianos''', que se quer rotacionar o objeto, | |
| − | + | ''sin'' é a operação do seno sobre o ângulo e | |
| − | + | ''cos'' é a operação do cosseno sobre o ângulo. | |
| − | |||
| − | |||
Logo, a fórmula matemática da operação de translação fica da seguinte forma: | Logo, a fórmula matemática da operação de translação fica da seguinte forma: | ||
| − | < | + | <math> |
| − | + | \begin{pmatrix} | |
| − | + | x & y | |
| − | </ | + | \end{pmatrix} |
| + | \cdot | ||
| + | \begin{pmatrix} | ||
| + | \cos(\theta) & \sin(\theta) \\ | ||
| + | -\sin(\theta) & \cos(\theta) \\ | ||
| + | \end{pmatrix} | ||
| + | </math> | ||
tal que: | tal que: | ||
| − | < | + | <math> |
| − | x' = (x | + | x' = (x \cdot \cos(\theta)) + (y \cdot -\sin(\theta)) |
| − | y' = (x | + | </math> |
| − | </ | + | |
| + | <math> | ||
| + | y' = (x \cdot \sin(\theta)) + (y \cdot \cos(\theta)) | ||
| + | </math> | ||
{{note|Observe que agora temos x' e y'. Isso por que em ambas as oeprações estamos utilizando o x e y originais. Se modificarmos o x na primeira operação, na segunda ele já vai estar modificado, o que distorce o elemento. A solução é criar variáveis auxiliares para não alterar os valores originais até o término do processo.}} | {{note|Observe que agora temos x' e y'. Isso por que em ambas as oeprações estamos utilizando o x e y originais. Se modificarmos o x na primeira operação, na segunda ele já vai estar modificado, o que distorce o elemento. A solução é criar variáveis auxiliares para não alterar os valores originais até o término do processo.}} | ||
Edição atual tal como às 09h29min de 18 de julho de 2023
Afluentes: Computação Gráfica
Representação
|
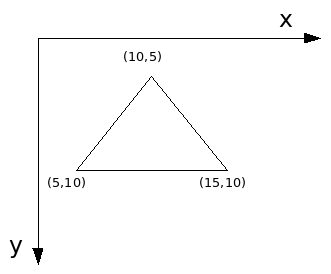
Por exemplo, se tivermos um triângulo, composto de três pontos e linhas ligando cada um dos pontos, então teremos:
Ponto {
Real x
Real y
}
Triangulo = Vetor [3] Ponto
Triangulo.Ponto[0]( 5, 10);
Triangolo.Ponto[1](10, 5);
Triangulo.Ponto[2](15, 10);
j = 1;
Para i = 0 até 2 Fazer
j = i + 1;
Se j > 2
Então j = 0
Fim se
Desenhar_linha(
Triangulo[i].Ponto.x, Triangulo[i].Ponto.y,
Triangulo[j].Ponto.x, Triangulo[j].Ponto.y)
Fim para
O código em C do arquivo ret.c apresenta a estrutura de um retângulo e uma operação de translação sobre a figura criada atraves da utilização das setas direcionais do teclado.
Transformações
As transformações são operações feitas nos objetos existentes, no plano bidimensional nesse caso, de forma que eles sejam modificados. Existem diversos tipos de operações, mas veremos apenas as transformações de translação, escala e rotação.
Translação
A translação no plano é a operação que move determinado objeto de um local à outro no no espaço bidimensional. A operação da translação ocorre com a soma da matriz de translação com todos os pontos do objeto. A matriz de translação é a seguinte:
tal que:
Tx é a translação na horizontal e Ty é a translação na vertical.
Logo, a fórmula matemática da operação de translação fica da seguinte forma:
tal que:
Algoritmo
Baseado na matriz e na fórmula para a operação de translação no plano, o algoritmo para esta operação fica da seguinte maneira:
Entrada Tx e Ty Para i = 0 Até Quantidade_de_pontos Fazer Ponto[i].x = Ponto[i].x + Tx Ponto[i].y = Ponto[i].y + Ty Fim para
Ou seja, a operação é executada em todos os pontos do elemento.
Exemplo
Agora imagine que vamos executar a operação de translação no nosso triângulo (Figura 1). Considere que vamos executar a operação de translação com os seguintes valores de Tx e Ty respectivamente (-2, 7). Então teremos que:
Ponto[0].x = Ponto[0].x + Tx = 5 + (-2) = 3 Ponto[0].y = Ponto[0].y + Ty = 10 + 7 = 17 Ponto[0].x = Ponto[0].x + Tx = 10 + (-2) = 8 Ponto[0].y = Ponto[0].y + Ty = 5 + 7 = 12 Ponto[0].x = Ponto[0].x + Tx = 15 + (-2) = 13 Ponto[0].y = Ponto[0].y + Ty = 10 + 7 = 17
Logo, nossos pontos passarão a ser:
Pontos (3, 17), (8, 12) e (13, 17)
Gerando uma nova imagem com o elemento Triângulo em uma nova posição.
Escala
|
A operação da escala ocorre com a multiplicação da matriz de Escala com todos os pontos do objeto. A matriz de escala é a seguinte:
tal que:
Sx : é a modificação da escala na horizontal e Sy : é a modificação da escala na vertical.
Logo, a fórmula matemática da operação de translação fica da seguinte forma:
tal que:
Algoritmo
Baseado na matriz e na fórmula para a operação de escala no plano, o algoritmo para esta operação fica da seguinte maneira:
Entrada Sx e Sy Para i = 0 Até Quantidade_de_pontos Fazer Ponto[i].x = Ponto[i].x * Sx Ponto[i].y = Ponto[i].y * Sy Fim para
A operação é executada em todos os pontos do elemento, assim como na operação de translação.
Exemplo
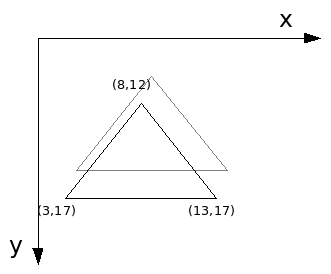
Agora imagine que vamos executar a operação de escala no nosso triângulo original (Figura 1). Considere que vamos executar a operação de escala com os seguintes valores de Sx e Sy respectivamente (0.5, 2). Então teremos que:
Ponto[0].x = Ponto[0].x * Sx = 5 * 0.5 = 2.5 Ponto[0].y = Ponto[0].y * Sy = 10 * 2 = 20 Ponto[0].x = Ponto[0].x * Sx = 10 * 0.5 = 5 Ponto[0].y = Ponto[0].y * Sy = 5 * 2 = 10 Ponto[0].x = Ponto[0].x * Sx = 15 * 0.5 = 7.5 Ponto[0].y = Ponto[0].y * Sy = 10 * 2 = 20
Logo, nossos pontos passarão a ser:
Pontos (2.5, 20), (5, 10) e (7.5, 20)
Gerando uma nova imagem com o elemento Triângulo com sua escala modificada.
|
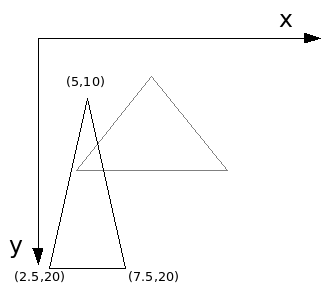
Neste caso, pegaremos o ponto 0 como pivot do objeto para mostrar o exemplo acima agora usando a operação sobre o pivot.
Sendo assim, nosso algoritmo fica da seguinte forma:
Entrada Sx e Sy Pivot = Ponto[0]; Transladar(-Pivot.x, -Pivot.y); Para i = 0 Até Quantidade_de_pontos Fazer Ponto[i].x = Ponto[i].x * Sx Ponto[i].y = Ponto[i].y * Sy Fim para Transladar(Pivot.x, Pivot.y);
Agora com essa operação de translação usando o pivot negativo, temos os seguintes pontos:
Pontos = (0, 0), (5, -5) e (10, 0)
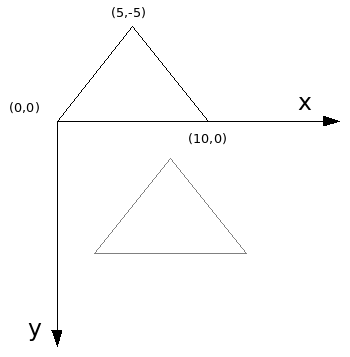
Só então aplicamos a operação de Escala, resultando os seguintes pontos:
Pontos = (0, 0), (2.5, -10) e (5, 0)
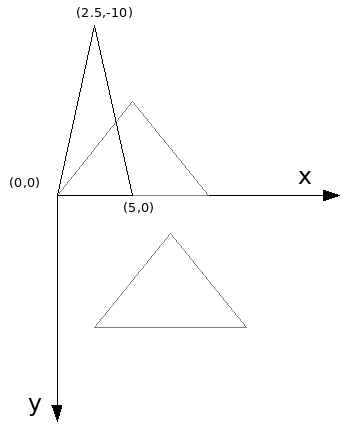
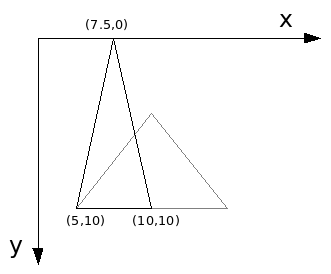
Depois disso então movemos de volta os pontos para o ponto de origem do objeto conforme a localização original do pivot, armazenada anteriormente. Obtemos então os seguintes pontos:
Pontos = (5, 10), (7.5, 0) e (10, 10)
Rotação
A rotação, no plano, é a operação que rotaciona determinado objeto no espaço bidimensional. A operação de rotação ocorre com a multiplicação da matriz de Rotação com todos os pontos do objeto. A matriz de rotação é a seguinte:

tal que:
θ é o ângulo, em radianos, que se quer rotacionar o objeto, sin é a operação do seno sobre o ângulo e cos é a operação do cosseno sobre o ângulo.
Logo, a fórmula matemática da operação de translação fica da seguinte forma:
tal que:
|
|
Algoritmo
Baseado na matriz e na fórmula para a operação de escala no plano, o algoritmo para esta operação fica da seguinte maneira:
Entrada ang Pivot = Ponto[0]; Transladar (-Pivot.x, -Pivot.y) Para i = 0 Até Quantidade_de_pontos Fazer xAux = (Ponto[i].x * cos(ang)) + (Ponto[i].y * -sen(ang)) yAux = (Ponto[i].x * sen(ang)) + (Ponto[i].y * cos(ang)) Ponto[i].x = xAux Ponto[i].y = yAux Fim para Transladar (Pivot.x, Pivot.y)
A operação é executada em todos os pontos do elemento, assim como na operação de translação e na escala.











