Perspectiva ou Projeção Cônica
Afluentes: Computação Gráfica
Introdução
Para representarmos um espaço tridimensional, da forma como é vista pelo olho humano, em um plano bidimensional, no caso a tela do computador, é utilizada uma das mais importantes descobertas no mundo das artes, da qual introduziu o realismo nas pinturas e desenhos.
A partir de análises visuais, a Perspectiva foi descoberta na busca de soluções geométricas para a construção da cúpula da Catedral de Florença pelo arquiteto italiano Brunelleschi (1377-1446).
A projeção perspectiva, produz uma imagem realista, porém não em suas verdadeiras medidas, executando uma operação dentro do espaço tridimensional para representar a cena vista de um ponto de observação a uma distância finita.
Na projeção perspectiva, as coordenadas dos pontos projetados são obtidas pela intersecção dos raios projetores com o plano de projeção, conforme visto na Figura 1.
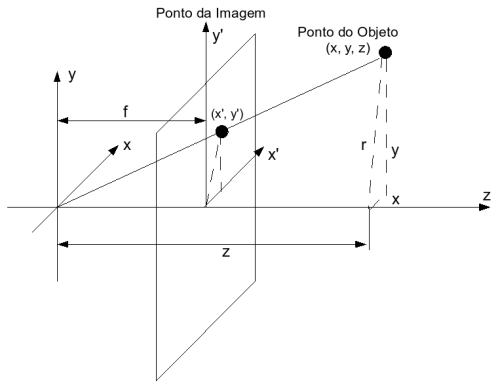
Sendo que:
- f é a distância do observador até o plano de projeção;
- z é a distância do observador até o ponto original;
- (x,y,z) é a localização espacial do ponto original;
- (x',y') é a representação do ponto original no plano de projeção, observando-se que o z não existe no plano de projeção, passando a ser z = 0;
Ao aplicarmos o ponto do objeto no plano da imagem, iremos criar o ponto de projeção. Dessa forma, estamos aplicando uma transformação do espaço tridimensional para o espaço bidimensional.
Simplificando todo processo para se chegar à representação do ponto (x, y) no plano de projeção (x', y'), temos as seguintes fórmulas:
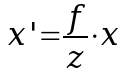
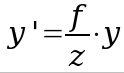
Sendo assim, devemos criar uma nova cena distorcida no espaço euclidiano, mas suficiente para criar uma representação no plano de projeção. Dessa forma, vamos criar uma representação de cada elemento da cena em que para cada ponto do elemento vamos aplicar as fórmulas acima.
Distancia = 300 Elemento2 = Elemento Para i = 0 Até Quantidade_de_pontos Fazer Elemento2[i].x = ( Distancia / Elemento[i].z ) * Elemento[i].x; Elemento2[i].y = ( Distancia / Elemento[i].z ) * Elemento[i].y; Fim para
Tendo sido criado um novo elemento (Elemento2), que é a representação do elemento original (Elemento) no plano de projeção, então não mais iremos apresentar o elemento original, mas apenas o elemento que é a sua representação no plano de projeção.
O resultado do algoritmo aplicado em um objeto tridimensional (cubo), originalmente no espaço euclidiano (Figura 2), é apresentado na Figura abaixo.
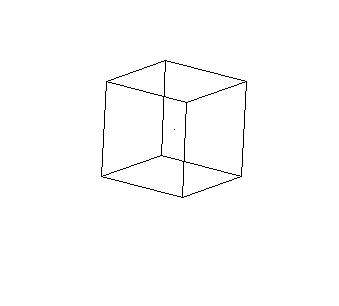
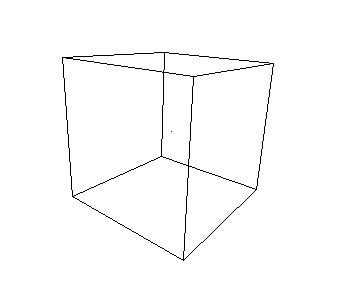
Implementação
Arquivo space.py.
from __future__ import annotations
import sys
import math
import pygame
# Configuration
SPEED: float = 0.1
WIDTH: int = 800
HEIGHT: int = 600
Color_screen: pygame.Color = (255, 255, 255)
Color_line: pygame.Color = (0, 0, 0)
CONICAL: bool = False
DISTANCE: float = 300
# -------------------------
# Edge Point
# -------------------------
class Point:
def __init__(self, x: float, y: float, z: float):
self.x: float = x # vetor x
self.y: float = y # vetor y
self.z: float = z # vetor z
def copy(self) -> Point: # Cria uma copia do ponto
return Point(self.x, self.y, self.z)
# -------------------------
# Edge Cube
# -------------------------
class Cube:
def __init__(self, screen):
self.screen: pygame.display = screen # Referencia a screen do pygame
self.points: list[Point] = [ # Criacao dos pontos do cubo
Point(0, 0, 0),
Point(-50, -50, -50),
Point(+50, -50, -50),
Point(+50, +50, -50),
Point(-50, +50, -50),
Point(-50, -50, +50),
Point(+50, -50, +50),
Point(+50, +50, +50),
Point(-50, +50, +50)
]
self.translate(0, 0, 300) # Move para uma posicao inicial longe da tela
def translate(self, tx, ty, tz) -> None: # Translada o cubo
for p in self.points: # Para cada ponto executa a matriz de translacao
p.x += tx # Soma x a tx
p.y += ty # Soma y a ty
p.z += tz # Soma z a tz
def scale(self, sx, sy, sz) -> None: # Executa a escala no cubo
pivot = self.points[0].copy() # Cria uma copia do ponto pivo
self.translate(-pivot.x, -pivot.y, -pivot.z) # Translada para a origem com referencia ao pivo
for p in self.point: # Executa a matriz de escala para cada ponto
p.x *= sx
p.y *= sy
p.z *= sz
self.translate(pivot.x, pivot.y, pivot.z) # Translada da origem de volta ao pivo original
def rotate(self, angle, axis): # Executa a rotacao do cubo
angle = math.radians(angle) # Converter para radianos
pivot = self.points[0].copy() # Faz uma copia do ponto pivo
self.translate(-pivot.x, -pivot.y, -pivot.z) # Translada para a origem com referência ao pivo
for p in self.points: # Executa a matriz de rotacao em cada ponto e cada vetor
x, y, z = p.x, p.y, p.z
if axis == "x":
p.y = y * math.cos(angle) - z * math.sin(angle)
p.z = z * math.cos(angle) + y * math.sin(angle)
elif axis == "y":
p.x = x * math.cos(angle) - z * math.sin(angle)
p.z = z * math.cos(angle) + x * math.sin(angle)
elif axis == "z":
p.x = x * math.cos(angle) - y * math.sin(angle)
p.y = y * math.cos(angle) + x * math.sin(angle)
self.translate(pivot.x, pivot.y, pivot.z)
def perspective(self, p) -> Point: # Executa visualizacao da projecao conica / perspectiva se ativa
if CONICAL and p.z != 0:
scale = DISTANCE / p.z
return Point(p.x * scale, p.y * scale, p.z)
return Point(p.x, p.y, p.z)
def line(self, p1, p2) -> None:
pygame.draw.line(self.screen, Color_line, (p1.x, p1.y), (p2.x, p2.y))
def draw(self) -> None: # Desenha o cubo
p = []
for i in range(9):
point = self.perspective(self.points[i])
point.x += WIDTH / 2
point.y += HEIGHT / 2
p.append(point)
self.screen.fill(Color_screen)
self.line(p[0], p[0]) # draw point over pivot
for i in range(3):
self.line(p[i + 1], p[i + 2])
self.line(p[i + 5], p[i + 5 + 1])
self.line(p[i + 1], p[i + 5])
self.line(p[4], p[1])
self.line(p[8], p[4])
self.line(p[5], p[8])
pygame.display.flip()
def change(self, move):
if move == "translate_left":
self.translate(-SPEED, 0, 0)
elif move == "translate_right":
self.translate(SPEED, 0, 0)
elif move == "translate_up":
self.translate(0, -SPEED, 0)
elif move == "translate_down":
self.translate(0, SPEED, 0)
elif move == "translate_front":
self.translate(0, 0, SPEED)
elif move == "translate_back":
self.translate(0, 0, -SPEED)
elif move == "rotate_y_left":
self.rotate(-SPEED, "y")
elif move == "rotate_y_right":
self.rotate(SPEED, "y")
elif move == "rotate_x_up":
self.rotate(SPEED, "x")
elif move == "rotate_x_down":
self.rotate(-SPEED, "x")
elif move == "rotate_z_right":
self.rotate(SPEED, "z")
elif move == "rotate_z_left":
self.rotate(-SPEED, "z")
def main():
global CONICAL
screen = pygame.display.set_mode((WIDTH, HEIGHT))
cube = Cube(screen)
cube.draw()
move = ""
while True:
for event in pygame.event.get():
if event.type == pygame.QUIT:
sys.exit(0)
elif event.type == pygame.KEYDOWN:
if event.key == pygame.K_LEFT:
move = "translate_left"
elif event.key == pygame.K_RIGHT:
move = "translate_right"
elif event.key == pygame.K_DOWN:
move = "translate_down"
elif event.key == pygame.K_UP:
move = "translate_up"
elif event.key == pygame.K_q:
move = "translate_back"
elif event.key == pygame.K_e:
move = "translate_front"
elif event.key == pygame.K_a:
move = "rotate_y_left"
elif event.key == pygame.K_d:
move = "rotate_y_right"
elif event.key == pygame.K_w:
move = "rotate_x_up"
elif event.key == pygame.K_s:
move = "rotate_x_down"
elif event.key == pygame.K_x:
move = "rotate_z_right"
elif event.key == pygame.K_z:
move = "rotate_z_left"
elif event.key == pygame.K_c:
CONICAL = not CONICAL
elif event.key == pygame.K_ESCAPE:
sys.exit(0)
elif event.type == pygame.KEYUP:
move = ""
cube.change(move)
cube.draw()
if __name__ == "__main__":
main()